Střed úsečky
Střed úsečky půlí úsečku na dvě stejné velké části. Pokud znáte dva krajní body úsečky, není problém střed spočítat.
Střed úsečky v rovině
Podobně jako u počítání vzdáleností dvou bodů si i počítání středů úseček rozdělíme na podkategorie.
Mějme body A[a1; a2] a B[b1; b2]. Určete jejich střed.
Střed dělí, jak už jsme si řekli, úsečku na dvě stejné části. Z toho vyplyne vzorec: S[(a1+b1)/2; (a2+b2)/2]. Měli bychom si to ihned vyzkoušet na nějakém příkladu. Na předchozím obrázku byli body A, B zadány: A[1; 3] a B[3; 1]. Určete střed úsečky AB.
![S\left[\frac{a_1\ +\ b_1}{2};\ \frac{a_2\ +\ b_2}{2}\right]](data:image/gif;base64,R0lGODdhmAAnAPMAAP///9XV1crKysDAwLW1tampqZ6enm5ubmJiYlRUVEZGRjg4OCgoKAAAAAAAAAAAACH5BAEAAAAALAAAAACYACcAAAT/EMhJa7u36s27/2AojiOWkQ2prmzrvin6znRth3F5uw2S70BK7/chgow3JKcxCLKUG6ZO5gRANdfqcirKYrXeSVgr5OJUyMBlMI6KBolLwKVmtr8huPxMpagFbAI8IgcIA2wTiCJ/gYMhhYcxdQ1zFmhYglZoJgomUFKaVj0lmXeiGJ0mHaAxUoplfWKyiXdjOT9ttxOTlUdds7qWsRIxAg2lo2YexbhTxqVNr0W/AMZ4sMpWA8YGzdlL25TYR+HdxLO+OOG9EtbC2XVs3tQgdeyhIfEn48uLe37i3tHjM/CJDXfpWvxxM2waGYF0ApIxVoCAESXGMFg8983JBR+m+iosfGgF5MUNcTINQHCAY0GSMyhuhLlKA5smYkp1GRKSJhaTPrdUQKAA57WgSJMypICAQQKj/JTulFrDiIAEDBb0yORSjKevYMOKHRuW2CeyaNOqxXB0ggAfCxggiEq1LsksWuna3evxQ4K56G7w4psPwz0bPxASg9qzSBNjhwlbeCwxCQVI7RokgFjVbWMsnxMqRizEIgaugUmndoFgc5V5lhvuGO1CmhbaNEyFPoJ6xu4uvTvLPvjbM0ncuS85GVk18g7mO3QvF1ccppo51fXWBEKxq2QN3fHF7gjDZHYyPPeNf/m9PQzl7uO/Hy6/fsKdbO3rj6IKQAQAOwAAAAAAAAAAAA==)
![S\left[\frac{4}{2};\ \frac{4}{2}\right]\\S[2;\ 2]](data:image/gif;base64,R0lGODdhOAA4APMAAP///+Xl5eLi4t3d3dXV1crKysDAwLW1tampqW5ubmJiYlRUVEZGRjg4OCgoKAAAACH5BAEAAAAALAAAAAA4ADgAAAT/EMhJ57u36s03zp0VjiT3lGcHltRapSOsFcvCUrTtoRzxILKSD2jiaXwEQHCEVBZJy8KjIFl2pFTnDqpRMEQsL1hjJZMXGIZLhb6ol+VX7CbfSqSYQypepbeeAGhZBgoJfSF8iE8GDwYtWXEXCmsxD5NwEl6Odn6dYAoOC5t1LJR+KTQODZZZhy0fGFWRsJQwBZMNDgp/nr1aFau8vp1WC7tjFD4XSTfKD8xkUi+jvy2OUtBQ188eCQqbUjrIY9KyindWF3oYreOuvwrinOlGVzCMLOWk5yrtiRbtJAz4V22GDH0hEE4QQDCOD3/ZekzZEKChxCQEJzRZUrEejh/v0EZIQRASAEOPFi6ZMqFyyUCUw0rBjMkFygeaKm7i3Mmzp8+fQIMKBaoTZ1FiQv/hUbcnGYaIIZxlSyRIAiFDv6Q4YhSQg1YAXN1RYERtIjxxCbCOiDchrdgJmgC5aCgDBh9QojhRYKskI9+CFVKtUuCPgzFzJQ6XDIxLl7CPXUWaBdwhmLsmdDAvNnwspGYWnykDUNjoMeaMp996A/dAXlaQh1aOhv2rzIN1F7rabZniLxneb2dWwIe0l8XinpRm3HcKANQWz6OKRhFr51EKEQAAOwAAAAAAAAAAAA==)
Střed úsečky v prostoru
Pokud již umíme počítat střed úsečky v rovině, není problém spočítat střed úsečky v prostoru.
Do vzorečku přibude akorát průměr z-ových souřadnic bodů:
![S\left[\frac{a_1\ +\ b_1}{2};\ \frac{a_2\ +\ b_2}{2};\ \frac{a_3\ +\ b_3}{2}\right]](data:image/gif;base64,R0lGODdh2AAnAPMAAP///9XV1crKysDAwLW1tampqZ6enm5ubmJiYlRUVEZGRjg4OCgoKAAAAAAAAAAAACH5BAEAAAAALAAAAADYACcAAAT/EMhJZ7u36s27/2AojmRpniCWhQ3qvnAsz3QqtnWu73xP4jYfCwEUzhpEYw1Z/DQ7T1qU0xgogyzr1TPdVEfdShg2ppSvZ0nauF4D0u5Se+sE07n2PJYSuAziZiIDCRcBLn1VgBaChA2GKIh/LmmDhSw3Gn0CfwKTIgcIA5ISoyGanJ4hoKI4iI6mDZuxqSCro66PgZdinW9yKgoqXV++b0hgvXHCwSpQWjhfpVzJvxjMGM5qap3S2ru6xaRucIvl30C4mOfe4Xjs6d917Ob07roCs8YIP+r44EH4klnpBqXfkzM4Am4DQJCKwQoEyYkZgM9AkXE3KL6qx0WjRXYS/1NozCXBn8iKB9Wd3GiM2D97EyKtmLfHAyKS7T7ITBnPpiU+LH0matLQi4ibGiKq7CmPFgyTNUtoIuNnqRyOIZn6UJQpKA98BQhwpVB0yUCeE/BhEEuzqZALRMYCmMom7lggco9iwNmOUK8BCA60hXnnBFi2hU9EyxsDyB8tC3NCYcIYjd3EJ+BhDodAAWQxm0OLHq0SAYMEnzmS9lKZzszV/EomYLAASa+2wnLr3s27N281w3wLH04cm7HJxZMrbwY6LZEFDPaphk29upIptV9a385dx5QE0gfD0NxdAvny548AgKrmc2szVvDx3f5FfnkL8b3KaLGqZIMEzS2RVp5rr+UABHsvFCigf969IRYGt02XoHYoIAAgDxfNYGEPGRpoVQ4IulBWDSGiMCINJZLx4RIRqshGixO+2KBWM6Ro2Hsd2GiCjjXiKGGAOdC133w1CNkYkTQYKcWKMfRhiI89OCkZd1JCmVWPBYhXHVhaUsfllC5G1ZhdUO5AmYL0kTmjmPe16SaNGpT55pyYXUnnnXjCwRyefHYnDAARAAA7AAAAAAAAAAAA)
Vypočtěte střed úsečky A[1;2;3] a B[4;5;6]
![S\left[\frac{5}{2};\ \frac{7}{2};\ \frac{9}{2}\right]](data:image/gif;base64,R0lGODdhSAAgAPMAAP///+Xl5eLi4t3d3dXV1crKysDAwLW1tampqW5ubmJiYlRUVEZGRjg4OCgoKAAAACH5BAEAAAAALAAAAABIACAAAAT/EMhJ57u36s27p1j2Ac9onqhllin3GO0qV69UsJ8SiiNxERucRyjRYYAjIYLI8RVuSNBM2sL5osOCjckMarqoh3ZK+pIlj+UDa7qFx2XamSSGpsQo501hTnrcJ4B5F0t9H2AqJ3gxAAZcFDcYByyPW2GMaHCJAAuLBgoJaF8wdopVWo5ejTUWY0w+P3ctsGuqCgwwqpi7pgAKDgu5ciuIHTwxLAULDg0PCppcO2iIOyLHNNLDAAU6DQ58m7zixhvNVOPohhQL4KIVtGwd8IOxX4JownEgpLVJ/PEu/n1JoCDXjQXaNgG6dk4QQ4XRJmHQ5O5cHAUIXZzDSC5cxSF/YFikGiFo5Id7AHzMAQGnWCuLxigOcPmxgiCUG+7h1IBTAE197xaRAEjBCQiiE4xWCPCzyxWgHp7+lCC1gs85NxDU5JB1K9c0NWfOcRZihZGHQc4SUeknnVuPLsq+xbQjAgA7AAAAAAAAAAAA)
Ale existují i trochu složitější příklady. Vypočtěte souřadnice bodu B, jestliže víte, že bod A má souřadnice [7;8;9] a středem úsečky AB je bod S[0,1,2]:
b1 = s1*2-a1 b2 = s2*2-a2 b3 = s3*2-a3 b1 = -7 b2 = -6 b3 = -5 B[-7; -6; ;-5]
Máme trojúhelník ABC. Bod A má souřadnice [0;0], bod B[5;1] a bod C má souřadnice [4;4]. Vypočtete velikost těžnice ta:
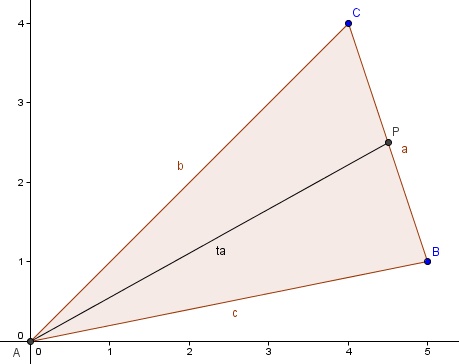
Využijeme toho co víme o těžnici. Těžnice vede ze středu strany do protějšího vrcholu. Jakmile tedy najdeme patu těžnice, nebude problém dopočítat velikost těžnice pomocí znalostí z předchozího článku, tedy počítání vzdálenosti bodů.
Nejprve tedy najdeme patu těžnice, střed úsečky BC.
P=[(5+4)/2; (1+4)/2] P=[4.5; 2.5]
Nyní stačí spočítat vzdálenost bodu P a bodu A:
|PA| = √((4.5-0)2+(2.5-0)2) |PA| = 5.15
Velikost těžnice ta je 5.15.
: