Pokud máme přímku p a body A, B, tak můžeme pomocí obecné rovnice přímky p určit, jestli se oba body nacházejí ve stejné polorovině (rovina je rozdělena na dvě poloroviny přímou p), popř. je-li každý v jiné polorovině. Takže my nedokážeme určit, jestli je bod nalevo nebo napravo od přímky, my pouze určujeme, zda se oba body nacházejí ve stejné polorovině. K čemu to je? Například proto, abychom otestovali, zda bod X leží/neleží v trojúhelníku ABC.
Začneme těmi nejjednoduššími příklady. Narýsujte přímku procházející body X[0,0], Y[1,1]:
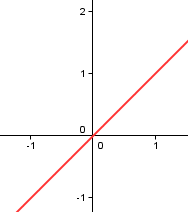
Tato přímka má obecnou rovnici p: x-y=0. Pokud do této rovnice dosadím souřadnice jakéhokoliv bodu, který leží na přímce, rovnice se potvrdí (0=0). Pokud tam ale dosadím souřadnice bodu, který na přímce neleží, rovnost nebude platit. Narýsujte si další dva body A[0, 2], B[2, 0].
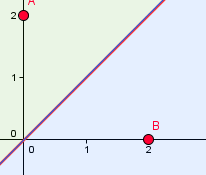
Nyní zkuste dosadit souřadnice bodů A, B dosadit do obecné rovnice přímky p:
A p: x-y=0 -2=0 B p: x-y=0 2=0
O bodech A, B se dá s pomocí obrázku s jistotou říci, že neleží ve stejné polorovině. To se nám také potvrdilo předchozím výpočtem. Totiž, pokud jsme do obecné rovnice přímky p dosadili souřadnice bodu A vyšla nám nerovnice -2 < 0 a pro bod B vyšlo 2 > 0. Rozdíl je jasný. Aby bod ležel v polorovině dané bodem A musí vyjít x < 0. A aby nějaký bod ležel ve stejné polorovině jako bod B, musí vyjít x > 0.
Leží bod M[4, 7] ve stejné polorovině jako bod N[5, 3] (pracujeme se stejnou přímkou jako v předchozím příkladě)?
Je zbytečné si kreslit obrázek, vše můžeme bez problému spočítat:
p: x-y=0 M 4-7=0 -3 < 0 N 5-3=0 2 > 0
Body M, N neleží ve stejné polorovině.
Složitější příklady
1) Určete, zda se bod M[3, 2] nachází v konvexním úhlu AVB.
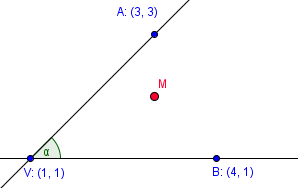
Trošku jsem vám zlehčil práci; podle obrázku totiž víte, že se bod nachází nachází v konvexním úhlu AVB. Na vás je pouze dokázat stejnou skutečnost numerickým výpočtem.
Začneme tím, že si napíšeme obecné rovnice přímek AV, BV.
AV: x-y=0 BV: 0x+y-1=0
Konvexní úhel AVB je vlastně průnik dvou polorovin (AVB a BVA). Bod M tedy musí splňovat dvě podmínky. Musí ležet v polorovině AVB a současně musí ležet v polorovině BVA.
Do obecné rovnice přímky AV dosadíme bod M AV: x-y=0 3-2=0 1 > 0 Polohu bodu M zkontrolujeme pomocí bodu B AV: x-y=0 4-1=0 3 > 0
Ověřili jsme,o že se bod M nachází v polorovině AVB. Zbývá ověřit, zda je bod M i v polorovině BVA:
Do obecné rovnice přímky BV dosadíme bod M BV: 0x+y-1=0 1 > 0 Polohu bodu M zkontrolujeme pomocí bodu A BV: 0x+y-1=0 2 > 0
Bod M leží v konvexním úhlu AVB.
2) Určete, zda se bod M[2, 2] nachází v trojúhelníku ABC.
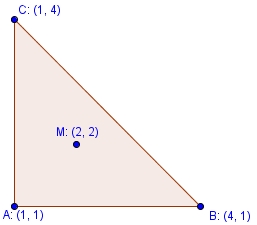
Trojúhelník je vlastně jenom průnik tří polorovin. Takže pokud bude bod M ležet ve všech třech polorovinách tak leží v trojúhelníku ABC. Je to vlastně předchozí příklad doplněný o ještě jednu polorovinu.
Opět začneme tím, že napíšeme obecné rovnice přímek:
AB: y-1=0 AC: x-1=0 BC: x+y-5=0
Postupně otestujeme, zda se bod M nachází ve stejné polorovině jako protější vrchol. Začneme přímkou AB.
Doplníme bod M do obecné rovnice přímky AB: AB: y-1=0 1 > 0 Doplníme bod C do obecné rovnice přímky AB: AB: y-1=0 3 > 0 → leží ve stejné polorovině
Tak, jedna podmínka je splněna. Nyní otestujeme polorovinu danou přímkou AC:
Doplníme bod M do obecné rovnice přímky AC: AC: x-1=0 1 > 0 Doplníme bod B do obecné rovnice přímky AC: AC: x-1=0 3 > 0 → leží ve stejné polorovině
I tato podmínka byla splněna. Nakonec otestujeme polorovinu danou přímkou BC:
Doplníme bod M do obecné rovnice přímky BC: BC: x+y-5=0 -1 < 0 Doplníme bod A do obecné rovnice přímky BC: BC: x+y-5=0 -3 < 0 → leží ve stejné polorovině
Bod M leží v trojúhelníku ABC.
Zdrojový kód
Zdrojový kód v jazyce C pro test, zda-li bod D leží v úhlu ABC :-)
int porovnej(long int u1, long int u2, long int u3, int a1, int a2, int b1, int b2){ /* * Zjistí, zda bodi A a B lezi ve stejne polorovine od primky u1x+u2y+u3=0 */ if ((u1*a1+u2*a2+u3) * (u1*b1+u2*b2+u3) > 0){ return 1; } return 0; } int v_uhlu(int a1, int a2, int b1, int b2, int c1, int c2, int d1, int d2){ /* * Kontroluje, zda lezi bod D[d1, d2] v uhlu ABC */ long int u[3] = {-b2+a2, b1-a1, 0};//primka AB - dosadit A, kontrola s C long int v[3] = {-c2+b2, c1-b1, 0};//primka BC - dosadit B, kontrola s A u[2] = -u[0]*a1-u[1]*a2; v[2] = -v[0]*b1-v[1]*b2; return (porovnej(u[0], u[1], u[2], c1, c2, d1, d2) && porovnej(v[0], v[1], v[2], a1, a2, d1, d2)); }
Toho, že umíme určit, zda-li se body nacházejí ve stejné polorovině se dá využít i v jiných příkladech než test toho, zda bod leží v trojúhelníku. Například pro test, je-li nějaký n-úhelník konvexní. Konvexní bude právě tehdy, bude-li pro každé jeho čtyři po sobě následující body platit, že první a čtvrtý bod jsou ve stejné polorovině dané přímkou, která vznikne spojením druhého a třetího bodu.