Z předchozích článků bychom již měli umět trochu pracovat s přímkou a právě díky parametrické rovnici přímky dokážeme vyjádřit parametrickou rovnici roviny.
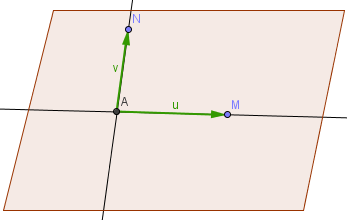
Označme u=M-A a v=N-A. Každý bod přímky AM můžeme parametricky vyjádřit jako:
M=A+u*t
A každý bod přímky AN můžeme vyjádřit jako:
A=N+v*s
Spojíte-li tyto dvě rovnice dohromady, dostanete rovnici:
M=N+v*s+u*t
Toto je parametrická rovnice roviny. Ale většinou se zapisuje ve tvaru:
X=A+u*t+v*s x=a1+u1*t+v1*s y=a2+u2*t+v2*s z=a3+u3*t+v3*s
Napište parametrickou rovnici roviny dané body A[1;2;-1], B[3;1;1], C[-1;1;0].
Nejprve musíme určit vektory u, v:
u=B-A u=(2;-1;2) v=C-A v=(-2;-1;1)
Parametrické rovnice přímek určujících rovinu jsou:
B=A+u*t A=C+v*s
Parametrická rovnice roviny ABC tedy je:
B=C+v*s+u*t x=-1+2t-2s y=1-t-s z=2t+s
Určete, zda bod X[-1;-1;3] leží v rovině z předchozího příkladu.
Aby bod X mohl ležet v rovině ABC, muselo by platit:
-1=-1+2t-2s -1=1-t-s 3=2t+s
Vypočtením prvních dvou rovnic dostaneme hodnoty t=1; s=1. Pokud tyto hodnoty dosadíme do třetí rovnice, dostaneme, že 3=3 a proto bod X leží v rovině ABC.
Jak lze vypozorovat z předchozího příkladu, rovinu je možné zadat i jinak než pomocí bodů. Rovinu lze zadat například pomocí dvou bodů a vektoru, bodu a dvou vektorů atd...
Procvičování
Následující příklady budou pouze obměny předchozího.
1) Zjistěte, zda bod M[3;0;1] leží v rovině ρzadané bodem A[1;1;3] a přímkou p(P, u), kde P[3;-1;-7] a u=(1;1;1).
Máme jednoznačně zadané dva body roviny (A, P) a jeden vektor(u), který také leží v zadané rovině. Do parametrické rovnice roviny potřebujeme určit ještě jeden vektor v:
v=P-A v=(2;-2;-10)
Nyní by neměl být problém napsat parametrickou rovnici roviny:
X=A+u*t+v*s x=1+t+2s y=1+t-2s z=3+t-10s
Aby bod M mohl ležet v rovině ρ, muselo by platit:
3=1+t+2s 0=1+t-2s 1=3+t-10s
Vypočtením prvních dvou rovnic dostaneme hodnoty s=3/4, t=1/2. Tyto hodnoty ale nepasují do třetí rovnice a proto bod M neleží v rovině ρ.
2) Určete poslední souřadnici bodu D[2;1;z], tak aby ležel v rovině ρ dané body A[1;1;0], B[3;1;-1], C[-1;1;2].
Opět musíme určit parametrickou rovnici roviny ρ:
u=B-A u=(2;0;-1) v=C-A v=(-2;0;2) X=A+u*t+v*s x=1+2t-2s y=1 z=-t+2s
Aby bod D ležel v rovině ρ, muselo by platit:
2=1+2t-2s 1=1 z=-t+2s
Vznikly nám dvě rovnice o třech neznámých. Z první rovnice si vyjádříme t=(1+2s)/2. Pokud tuto hodnotu dosadíme do třetí rovnice, dostaneme z=(-1+2s)/2 a proto můžeme z vybírat z intervalu všech reálných čísel.
3) Zkusíme si vypočítat obdobu předchozího příkladu. Určete třetí souřadnici bodu D[3;-2;z], tak aby ležel v rovině ρ dané body A[4;-1;2], B[5;2;0], C[0;1;-4].
Určíme parametrickou rovnici roviny ρ:
u=B-A=(1;3;-2) v=C-A=(-4;2;-6) X=A+u*t+v*s x=4+t-4s y=-1+3t+2s z=2-2t-6s
Dosadíme souřadnice bodu D:
3=4+t-4s -2=-1+3t+2s z=2-2t-6s
Z prvních dvou rovnic dostaneme t=-3/7, s=1/7. Dosazením do třetí rovnice získáme výsledek z=2.