Po delší pauze opět přichází článek o stereometrii. Dnešní téma tedy bude výpočet vzdálenosti bodu od přímky. Postup je takřka stejný, jako při počítání vzdálenosti bodu od roviny (Vzdálenost bodu od roviny), ale radši si to vysvětlíme.
První příklad - vzdálenost bodu od přímky v krychli
Vypočtěte vzdálenost bodu A od přímky BH v krychli ABCDEFGH. Délka hrany |AB| = 6 cm.
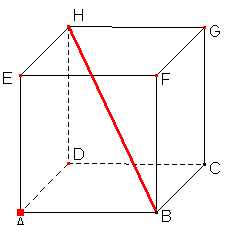
Podobně jako při řešení vzdálenosti bodu od roviny budeme i zde hledat pravoúhlý trojúhelník. V tomto případě půjde o trojúhelník ABP. Bod P leží na přímce BH a spojnice bodu AP je kolmá na přímku BH.
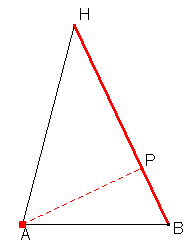
Z tohoto detailu už by mělo být každému jasné, co je potřeba spočítat. Velikost hrany AB známe, ale ještě musíme zjistit velikost úhlu |∠ABH|.
|AB| = 6 |AH| = √(62+62) = 8.48 |BH| = √(8.482+62) = 10.32 sin |∠ABH| = 8.48/10.32 |∠ABH|=55°24' |AP| = sin(|∠ABH|)*|AB|=4.93
Druhý příklad
Procvičíme si to na dalších příkladech. Určete vzdálenost bodu B od přímky AP v krychli ABCDEFGH. Bod P je střed hrany HG. Délka hrany |AB| = 6 cm.
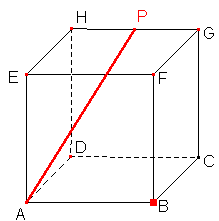
Musíme zjistit délku hrany AB a úhel ∠BAP. Délku hrany AB už známe, ale úhel musíme dopočítat. Nejlépe se tento úhel dá spočítat pomocí pravoúhlého trojúhelníku APS. Bod S umístíme do středu hrany AB.
|AS| = 3 |SP| = √(62+62) |SP| = √72 cos |∠BAP| = |AS|/|SP| |∠BAP| = 69°17' |BX| = sin(|∠BAP|)*|AB| |BX| = 5.62
Třetí příklad - vzdálenost bodu od přímky v jehlanu
V jehlanu ABCDV určete vzdálenost bodu S od přímky VC. Bod S leží na průsečíku uhlopříček v podstavě. Výška jehlanu v = 7 cm a délka hrany |AB| = 6 cm. Bod X je předpokládaný průsečík nejkratší vzdálenosti SX.
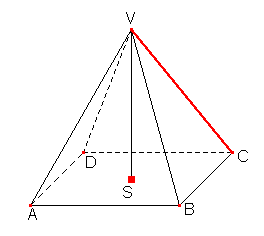
Musíme určit velikost úsečky SC, což je vlastně polovina úhlopříčky a ještě musíme určit velikost úhlu SCV. Tento úhel spočítáme z trojúhelníku SCV.
|SC| = |AC|/2 = √(62+62)/2 |SC| = 4.24 |CV| = 8.2 cos |∠SCV| = |SC|/|CV| |∠SCV| = 58° |SX| = |SC|*sin(|∠SCV|) = 4.24 * sin(58°) |SX| = 3.63
Čtvrtý příklad
V krychli ABCDEFGH určete vzdálenost bodu C od přímky AH. Délka hrany |AB| = 6 cm.
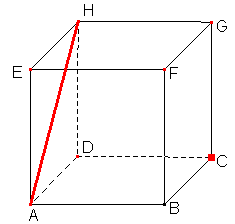
Musíme spočítat délku uhlopříčky |CA| a velikost úhlu ∠CAH. Oba výpočty jsou velmi jednoduché. Délku uhlopříčky jsme počítali v předchozích příkladech, takže |AC| = 8.5 a pokud se na obrázek dobře podíváte, zjistíte, že trojúhelník ACH je rovnostranný, tudíž |∠CAH| = 60°.
|CX| = sin(|∠CAH|) * |AC| |CX| = 7.36
Nyní už umíte počítat vzdálenost bodu od přímky.