Začneme opět pozorováním, na následujícím obrázku je dána krychle ABCDEFGH. Určete počet společných bodů s přímkou p.
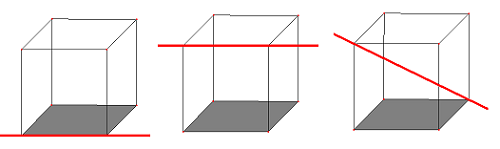
Na prvním obrázku leží přímka v rovině, má nekonečně mnoho společných bodů. Pokud by takovýto vztah nastal mezi dvěma přímkami, hovořili bychom, že jsou totožné, ale v případě roviny a přímky se o totožnosti nedá mluvit, proto můžeme konstatovat, že na prvním obrázku je přímka a rovina rovnoběžná. Na druhém obrázku nemá přímka a rovina žádný společný bod. V tomto případě tedy je přímka a rovina také rovnoběžná. Na posledním obrázku má přímka a rovina společný právě jeden bod a to je důkazem, že se jedná o stav různoběžnosti.
Víc se toho snad o vztahu mezi přímkou a rovinou nedá říci a tak sem pro vás na závěr připravil několik příkladů:
1) Je dána krychle ABCDEFGH. Určete všechny přímky, které procházejí bodem H a některým dalším vrcholem krychle a s rovinou ABC jsou různoběžné.
2) Je dána krychle ABCDEFGH. Určete všechny roviny, které prochází bodem H a dalším dvěma vrcholy krychle a jsou s přímkou BC různoběžné.
3) Je dána krychle ABCDEFGH. Určete všechny roviny, které prochází bodem H a dalším dvěma vrcholy krychle a jsou s přímkou BC rovnoběžné.